Add
Research
Research Interest
- Monetary and Fiscal Policy
- Monetary Policy Transmission
- Risk Management
- Financial Markets
- Market Structure and Pricing
- Foreign Reserves Management
- Debt Management
- Portfolio Optimization
Add
Publications

The present paper is focused on the solution of optimal control problems such as optimal acquisition, optimal liquidation, and market making in relation to the high-frequency trading market. We have modeled optimal control problems with the price approximated by the diffusion process for the general compound Hawkes process (GCHP), using results from the work of Swishchuk and Huffman. These problems have been solvedusing a price process incorporating the unique characteristics of the GCHP. The GCHP was designed to reflect important characteristics of the behaviour of real-world price processes such as the dependence on the previous process and jumping features. In these models, the agent maximizes their own utility or value function by solving the Hamilton–Jacobi–Bellman (HJB) equation and designing a strategy for asset trading. The optimal solutions are expressed in terms of parameters describing the arrival rates and the midprice process from the price process, modeled as a GCHP, allowing such characteristics to influence the optimization process, aiming towards the attainment of a more general solution. Implementations of the obtained results were carried out using real LOBster data.
Roldan Contreras, Ana, and Anatoliy Swishchuk (2022). “Optimal Liquidation, Acquisition and Market Making Problems in HFT under Hawkes Models for LOB” Risks 10, no. 8: 160. https://doi.org/10.3390/risks10080160.
Hawkes processes; general compound Hawkes processes; limit order books; optimal acquisition; optimal liquidation; market making optimization; high frequency trading; algorithmic trading; diffusion approximation of GCHP; LOBster data
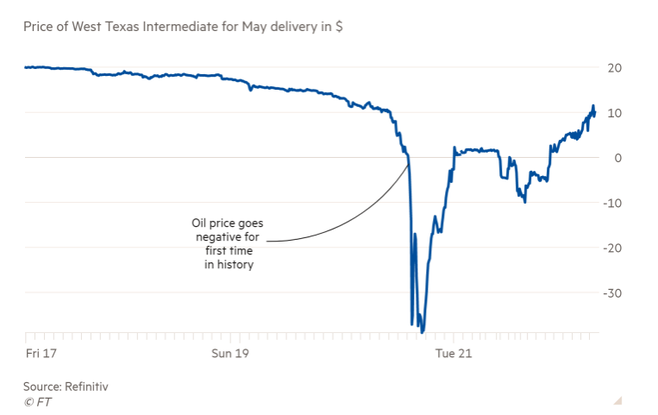
In this paper, we propose some alternatives to Black-76 model to value European options on future contracts in which the underlying market prices can be negative or/and mean reverting. We speci cally consider two models, namely Ornstein-Uhlenbeck (OU), for negative prices, and continuous-time GARCH (or inhomogeneous geometric Brownian motion), for positive prices. We then analyze the results and compare them with Black-76, the most commonly used model, when the underlying market prices are positive. Numerical examples are presented using WTI and NYMEX NG data sets.
Swishchuk, Roldan-Contreras, E. Soufiani, G. Martinez, M. Selfi, N. Agrawal, and Y. Yao, “Alternatives to black-76 model for options valuations of futures contracts”, Wilmott, vol. 2021, iss. 114, p. 40–49, 2021.
Add
Thesis Research
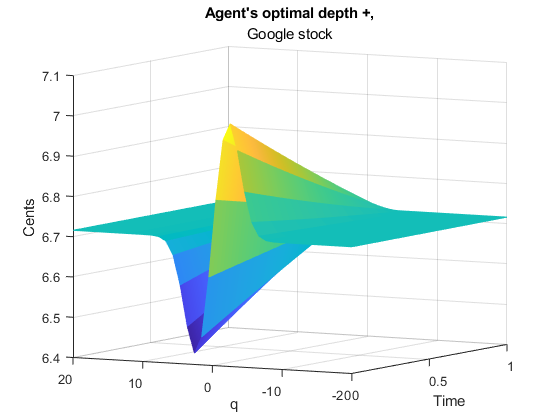
- This thesis is focused on the financial field of the High-Frequency Trading market.
- I solved innovative control problems for the optimal Liquidation, Acquisition and Market-Making problems and created general solutions.
- Modelled the price diffusion approximation with Markov, Semi-Markov and Hawkes compound processes.
- Implemented intensive programming tools on MATLAB along with the theoretical results, on the real-world information LOBster data.
- At the left, we can see the Optimal results for the Market Making problem for the Hawkes compound model for the Google stock. The optimal results come from a matrix where the trader places ask prices in the Limit Order Book according to the time and quantity of stocks to sell.
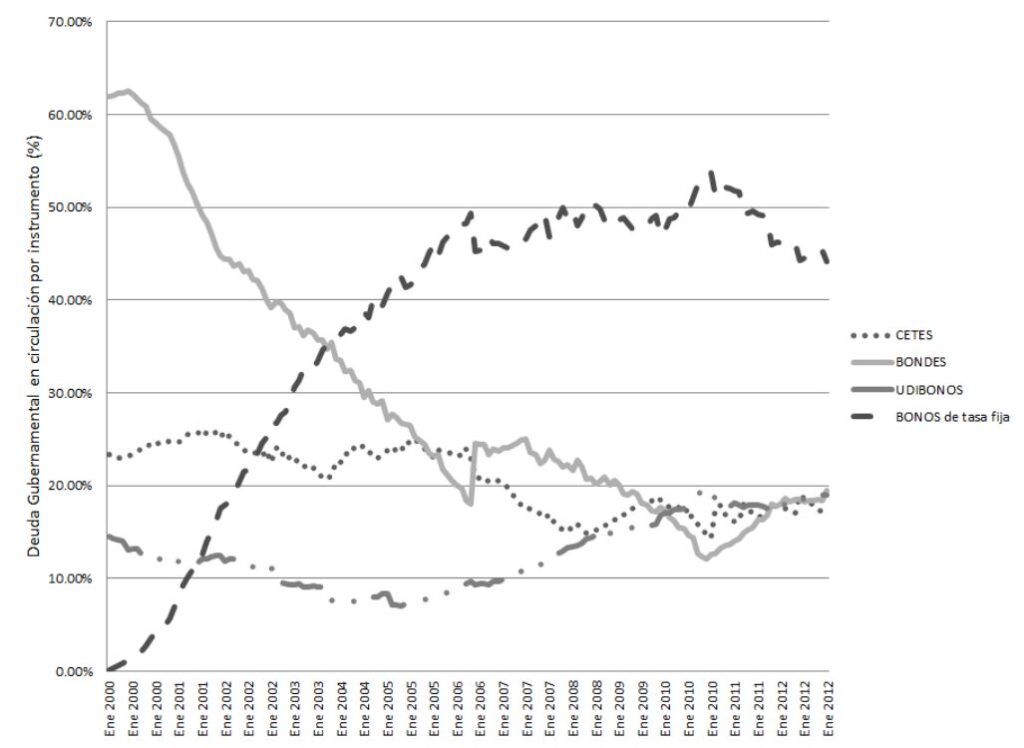
- This paper studies the Mexican bond market from the perspective of the term structure theory, which is known as “Preferred habitat.”
- We analyze how a positive or negative demand shock from a piece of the market with specific temporality affects interest rates and Bond market performance.
- Within the Preferred Habitat Theory, supply and demand shocks are absorbed by arbitrageurs’ customers; these shocks affect the term structure because arbitrageurs’ risk aversion makes them require a premium to absorb the shock.
- Consistent with the model, we found that a shock from a piece of the market with specific temporality (Mexican investment companies for retirement) positively affects interest rates and yield.
- At the left we can see Government Debt circulation percentage 2000-2012 by instrument. Source: Bank of Mexico